Wildfire resilience
Community resilience to wildfires - A network analysis approach by utilizing human mobility data
Chen, Q., Wang, B., & Crooks, A. (2024). Community resilience to wildfires: A network analysis approach by utilizing human mobility data. Computers, Environment and Urban Systems, 110, 102110.
Disasters have been a long-standing concern to societies at large. With growing attention being paid to resilient communities, such concern has been brought to the forefront of resilience studies. However, there is a wide variety of definitions with respect to resilience, and a precise definition has yet to emerge. Moreover, much work to date has often focused only on the immediate response to an event, thus investigating the resilience of an area over a prolonged period of time has remained largely unexplored. To overcome these issues, we propose a novel framework utilizing network analysis and concepts from disaster science (e.g., the resilience triangle) to quantify the long-term impacts of wildfires. Taking the Mendocino Complex and Camp wildfires - the largest and most deadly wildfires in California to date, respectively - as case studies, we capture the robustness and vulnerability of communities based on human mobility data from SafeGraph from 2018 to 2019. The results show that demographic and socioeconomic characteristics alone only partially capture community resilience, however, by leveraging human mobility data and network analysis techniques, we can enhance our understanding of resilience over space and time, providing a new lens to study disasters and their long-term impacts on society.
Highlights
- Quantifying community resilience is an open research challenge
- This paper develops a novel framework to quantify resilience after a disaster using network analysis
- Using human mobility data associated with two wildfires, we measure robustness and vulnerability of communities
- Results show community resilience is highly related to socio-economic and built environmental characteristics of the affected areas
- Our approach paves a way to study disasters and their long-term im- pacts on society
Introduction
Disasters, such as floods, earthquakes and wildfires have been a long-standing concern to societies across the globe. They often result in unpredictable effects on the environment, wildlife as well as human population. For example, disasters can disrupt transportation networks, supply chains, cause property loss, and can impact the biodiversity of a region. While taking wildfires as a disaster example, it is evident that, over recent decades, the frequency and impact of these events have not only increased in the United States but also in various parts of the world (e.g., Abatzoglou & Williams, 2016; Higuera, Abatzoglou, Littell, & Morgan, 2015; Running, 2006; USGCRP, 2018; Westerling, 2016). This trend perhaps best exemplified in countries like Greece and Spain, where multiple devastating wildfires have occurred in recent years, highlighting the global nature of this issue. The increasing occurrences of wildfires worldwide, driven by factors such as climate change and population growth, underscores the urgent need for a comprehensive understanding of community resilience to such extreme events. However, the exact definition of resilience has yet come to the consensus as it relates to a diverse set of determinants, ranging from individuals, society, to that of the economy and environment which all come into play when a disaster strikes (McCubbin, 2001; Southwick, Bonanno, Masten, Panter-Brick, & Yehuda, 2014; Yabe, Jones, Rao, Gonzalez, & Ukkusuri, 2022). That being said, in several disaster resiliency studies, one major notion of resilience stresses how well a system can re-establish stability and functions from the disruption of a disaster over time. For example, the National Academies (2012) defines disaster resilience as “the ability to prepare and plan for, absorb, recover from, or more successfully adapt to actual or potential adverse events.”
In this context, questions regarding how we quantify resilience to disasters have drawn attention from researchers across many disciplines. One commonly used approach is developing indices derived from different resilience determinants to evaluate and compare disaster resilience, such as the Baseline Resilience Index for Communities (BRIC) (Cutter, Burton, & Emrich, 2010), Community Disaster Resilience Index (CDRI) (Peacock et al., 2010), and Resilience Capacity Index (RCI) (Foster, 2012). These indices, and others alike, aggregate different metrics (e.g., social, economic, infrastructure, environment) to create a comparative resilience score, allowing the comparison of disaster resilience across space. However, their disadvantage relates to their performance in evaluating resilience which varies from one to the other, making the selection of the appropriate index to assist in emergency management and policy decision-making extremely difficult (Bakkensen, Fox-Lent, Read, & Linkov, 2017). Besides, as discussed above, each index is derived from multiple aggregated metrics, which makes the contribution of each metric unclear (Bakkensen et al., 2017). Moreover, such indices generally view resilience statically as an outcome for a specific moment in time. In other words, they overlook the dynamic changes of resilience over time (Southwick et al., 2014).
Another major focus of disaster resilience research is the study of human behaviors. Such studies aim to understand how people behave and interact with the built and natural environment in times of disasters from both individual and collective aspects. For example, in terms of collective behaviors, studies have uncovered the role of social relationships in supporting and adaptation in disasters (e.g., Aguirre, Wenger, & Vigo, 1998; Bolin, 2007; Drabek, Key, Erickson, & Crowe, 1975; Quarantelli, 1984). Regarding individual behaviors, research generally focuses on cognitive science, ranging from understanding how people react to stresses in disasters (e.g., Fritz & Marks, 1954; Glass, 1959; Quarantelli, 1954), to social/place attachments (e.g., Grinberger & Felsenstein, 2016; Hobfoll, 1989; Hobfoll, 2001; Mawson, 2005) and decision-making (e.g., Bandura, 2001; Benight & Bandura, 2004; Paton, 2003; Richard Eiser et al., 2012; Rosenstein, 2004). Although these studies provide more dimensions, such as perspectives of social norms, psychology, and social attachment, in disaster resilience research, they have mostly focused on the theoretical construction and/or conceptual modeling (Burger, Kennedy, & Crooks, 2021), where empirical validation still largely remains unexplored due to, for instance, the limitation of available data.
The advent of Web 2.0 and associated technologies (O’Reilly, 2006) has led to the emergence of “big data” which has proliferated due to location-based services, social media platforms (e.g., Twitter, Facebook) and mobile phone devices. They have produced data at an unprecedented scale, resulting in disaster resilience research shifting towards a more data-driven direction (Burger, Oz, Kennedy, & Crooks, 2019; Hsu, Liu, Nguyen, Chien, & Mostafavi, 2024). One major stream of this data- driven approach is the use of sentiment analysis techniques to investigate people’s opinions to disasters. For example, Yuan, Li, Liu, Zhai, and Qi (2021) utilized Twitter data to identify dynamic crisis response disparities and explore concern themes of individuals with different demographic characteristics (e.g., race, gender) during Hurricane Florence. Similarly, Yan, Chen, and Wang (2020) used geotagged Twitter data to identify and compare people’s sentiments and perspectives of post-disaster recovery process by using sentiment analysis and latent dirichlet allocation topic modeling after earthquakes in Lombok and Bali. Another stream focuses on human mobility analysis to monitor and compare individuals’ movements and behavioral responses to a disaster. For instance, Roy, Cebrian, and Hasan (2019) introduced the notion of mobility resilience to detect the ability of people to resist impacts of an extreme event (e.g., hurricane, earthquake, rain storm) by using geo-located social media data. Yabe, Zhang, and Ukkusuri (2020) studied business recovery in Puerto Rico after Hurricane Maria based on mobile phone data provided by Safegraph. Through the analysis of daily visits of establishments, they were able to quantify the disaster impacts to different types of businesses.
The above studies along with several others have illustrated the potential and flexibility of using big data to connect disaster information and people in times of crises, enhancing the understanding of disaster resilience. However, many studies have often focused on the short-term analysis (i.e., the response), which only covers one of the four stages of disaster management (i.e., mitigation, preparedness, response, and recovery). One reason for this is that analyzing resilience over a long-term period is still a challenge. Against this backdrop, we propose a novel framework that incorporates network analysis and the concept of the resilience triangle to capture potential impacts of dynamic disruptions of a disaster, especially on collective human behaviors to assess a community’s resilience to wildfires. Specifically, we employed degree centrality, a key metric in the network analysis, as a proxy for evaluating disaster resilience. The degree centrality reflects the extent to which a community-based group has been exposed to a disaster, where a higher degree centrality implies greater exposure. These measures have been applied in urban resilience studies, especially relating to topics around natural disasters, climate change, transport, urban forms and social ties (e.g., Akbarzadeh, Memarmontazerin, Derrible, & Salehi Reihani, 2019; Boulmakoul, Badaoui, Karim, Lbath, & Oulad Haj Thami, 2022; Kalpana, Jayasinghe, Abenayake, & Wijayawardana, 2021; Torres & Casey, 2017; Wang, Chen, Mu, & Zhang, 2020). By analyzing the dynamic changes in degree centrality of a community-based group, we are able to assess and quantify resilience in the face of wildfire disruptions in this paper.
Complementing our network analysis, we utilized the concept of the resilience triangle, which originated from the work of Bruneau et al. (2003), as a quantitative conceptual framework for measuring disaster resilience as shown in Fig. 1. The concept was then mathematically modeled by Tierney and Bruneau (2007) and Cimellaro, Reinhorn, and Bruneau (2010). In general, the resilience triangle can be used to measure the abrupt functionality loss of a social unit (e.g., a community) over time under the disruption of a disaster. The depth of the triangle (highlighted with red dashed line in Fig. 1) illustrates the severity of the disruption, the length of it demonstrates the recovery time, and the area of it indicates the resilience of the social unit. Fig. 1 (a) schematically represents the resilience triangle, where the y-axis depicts the quality of infrastructure (Q(t)) as a function of time, t0 marks the occurrence of a disruptive event, and t1 indicates the time when the infrastructure has completely recovered. In our study, we take into account the deteriorating situation as noted in the work of Hossain, Roy, Mohammad, Nawar, and Dipta (2021). Our rationale being that several studies have shown that the deteriorating situation is not an abrupt change but gradual drop after t0 (e.g., Roy et al., 2019), which is shown in Fig. 1 (b), specifically the path between A to B, where B is the lowest value at time tD - a point defined as “systemic impact” by Vugrin, Warren, Ehlen, and Camphouse (2010). This point represents the difference between the intended and actual performance levels following a disruption. Building upon the resilience triangle, resilience has been formally quantified as the ratio of the area of the triangle (the region shaded orange in Fig. 1(b)) to the total area under the pre-disruption level of performance, from the initial disturbance at t0 to the recovery at t1 (i.e., the sum of the areas shaded orange and green in Fig. 1 (b)) (Attoh-Okine, Cooper, & Mensah, 2009). A smaller ratio indicates a higher level of resilience (Labib, 2021).
In addition, the resilience triangle also allows us to capture two important features of resilience, namely robustness (referring to the ability of a social unit to cope with the impacts of disruption after a disaster) and vulnerability (which refers to the potential for loss (Cutter, Boruff, & Shirley, 2003)) of a social unit (see Fig. 1(b)). This triangle concept has been widely applied in different domains, such natural disasters (e.g., Hossain et al., 2021; Kahnamouei, Bolandi, & Haghifam, 2017; Mudigonda, Ozbay, & Bartin, 2019; Zobel & Khansa, 2014), supply chains (e.g., Adams, Bekkem, & Toledo-Dur’an, 2012; Bevilacqua, Ciarapica, & Marcucci, 2018; Pant, Barker, Ramirez-Marquez, & Rocco, 2014), civil infrastructure as well as economic systems (e.g., Yang & Frangopol, 2019), indicating the broad acknowledgement of the applicability of using the concept for quantifying resilience.
In this study, we evaluate the community resilience by combining network analysis, dynamic time warping clustering, as well as regression analysis techniques with the concept of the resilience triangle in space and time. Doing this allows us to answer questions, such as which community is more resilient compared to others and why? Did a community bounce back to its original status after a certain time or form a new normalcy under the effects of disruptions? What are the similarities and differences among communities? Answering these questions can help understand the resilience of each community, as well as the potential linkages between communities. Moreover, we argue that the proposed method can help scale up the concept of resilience to a more empirical framework that can be quantified and visualized through computational techniques assistance and data.
Figure 1. Resilience triangle. (a) The original resilience triangle (adapted from Bruneau et al., 2003); (b) The modified resilience triangle used in this study.
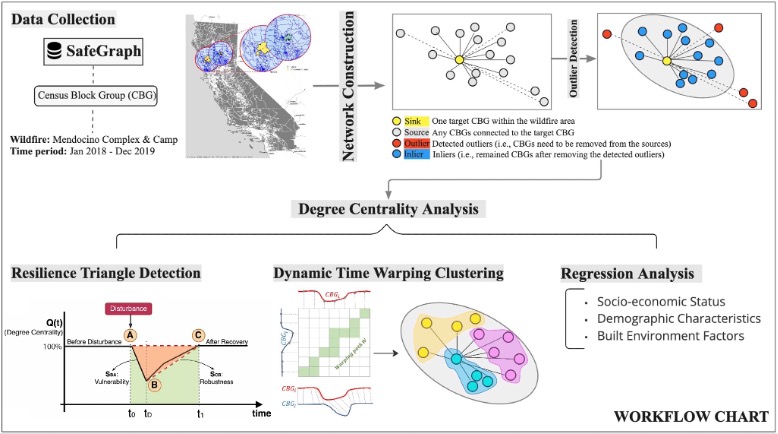
We borrows the concept of resilience triangle from disaster science to quantify resilience at the Census Block Group (CBG) level. The concept of resilience triangle was first introduced by Bruneau in 2003, to demonstrate a quantitative conceptual framework for measuring disaster resilience. In general, it can be used to measure the abrupt functionality loss of a social unit, like a community, over time under the disruption of a disaster. Besides, we also bring in the notion of degree centrality as a proxy for disaster resilience evaluation due to the consideration of the level of exposure of a CBG to a disaster. In other words, we take each CBG as a node and consider the connection between two CBGs as a link weighted by the frequency of visitation between the two. A node with high degree centrality indicates higher probability to be disrupted when being hit by a disaster. Therefore, we are able to identify the resilience triangle for each CBG.
Figure 2 gives two examples of detected traingles. The green dash line represents the pre-wildfire baseline level, which is defined as the two-month average degree centrality right before a disaster happens. It is considered as normal status and used to evaluate the recovery status.
- \(t_0\) is defined by the onset of a disaster;
- \(t_1\) is the time when the degree centrality reaches its minimum value between \(t_0\) and \(t_2\);
- \(t_2\) is the time when the degree centrally fully bounces back to the pre-wildfire baseline level, the green dash line aforementioned. However, if a CBG never fully restores to the baseline level, in this case, \(t_2\) is assigned by to the time when the maximum degree centrality occurs after the wildfire becomes inactive and we call this new normalcy.
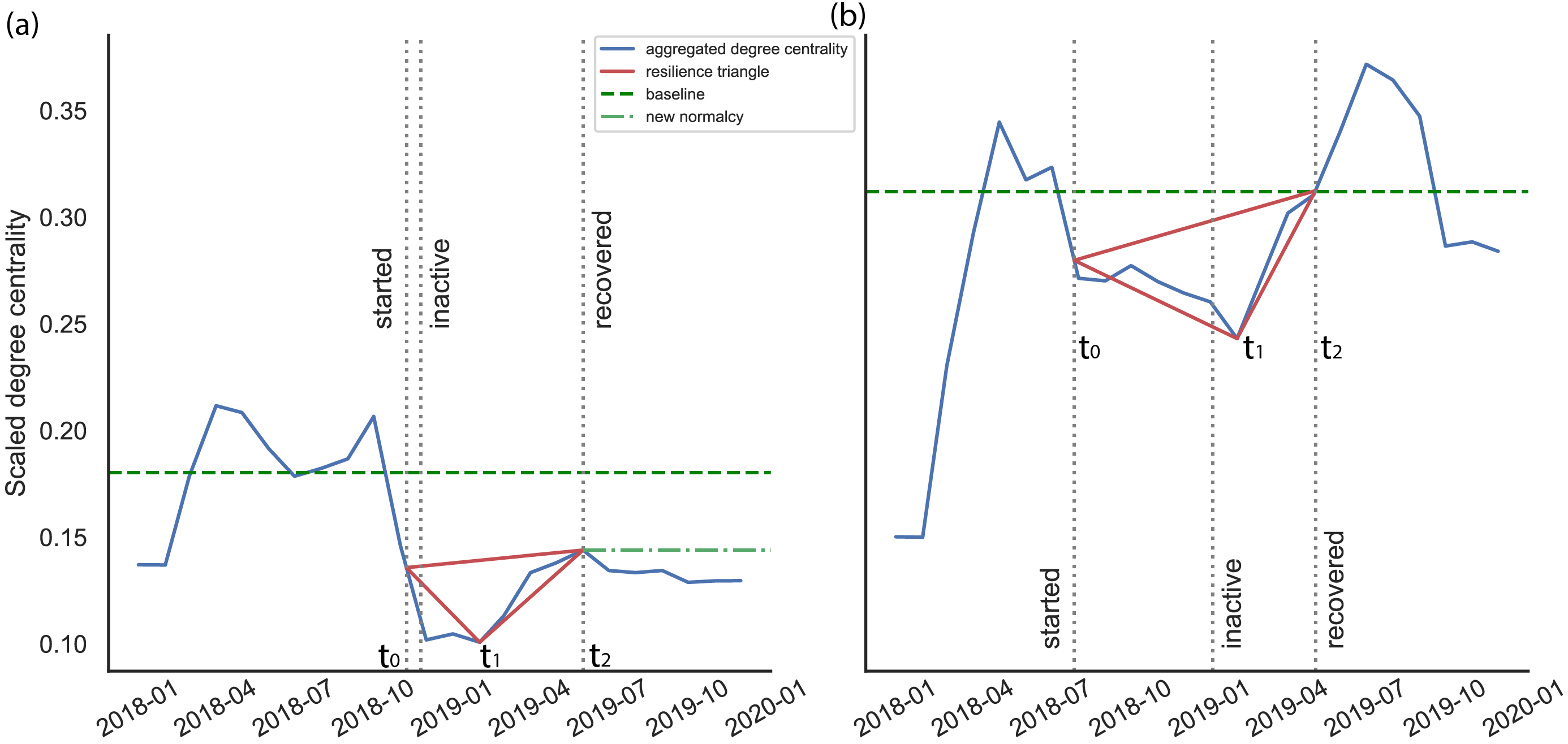
Figure 2. Triangle detection on the average degree centrality of CBGs within the two wild- fires. (a) Camp wildfire where baseline is not restored; (b) Mendocino Complex wildfire where baseline is restored.
As there can be many CGBs within the wildfire areas, which makes the comparison between CBGs become difficult. To overcome this challenge, we used Dynamic Time Warping (DTW) clustering, which is known as an accurate method for clustering time series data, to classify CBGs based on their changing patterns of degree centrality. Figure 3 denibstrates the temporal distribution of the degree centrality for every CBG within each wildfire area from January 2018 to December 2019 colored by different clusters. As the MC and Camp wildfires started on August 2018 and November 2018, respectively, we observe a sharp decline in the degree centrality after the onset of the events, indicating the immediate impacts of disruptions caused by the wildfires on human movements. Afterward, the degree centrality continues to decrease and reaches its lowest point after a period of time. Then, it gradually bounces to its pre-wildfire status or establishes a new normalcy.
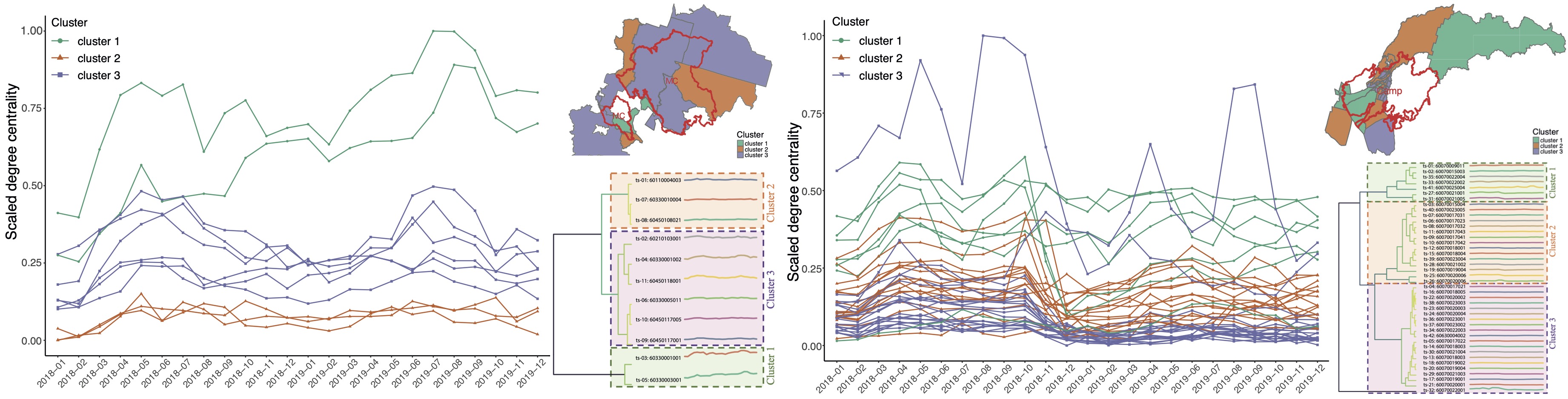
Figure 3. The distribution of degree centrality for each census block group colored by different clusters. (a) The Mendocino Complex wildfire; (b) The Camp wildfire. (Note: the degree centrality is normalized by using min-max normalization to ease comparison.)
Figure 4 displays resilience triangles for each CBG (i.e., lines with transparent color) and the overall resilience triangles for the three clusters (i.e., triangles with non-transparent color). The resilience triangle records the abrupt losses in performance of a social unit (here referring to a CBG) under the disruption of a disaster. The depth of the triangle illustrates the severity of the disruption, the length of it demonstrate the recovery time, and the area of it indicates the resilience of the social unit. The smaller the area is, the more resilient the social unit is. By comparing the derived resilience triangles, we find that cluster 2 is most resilient cluster, followed by cluster 3 and cluster 1 in the Camp wildfire. In terms of the MC wildfire, cluster 1 is the most resilient, followed by the clusters 3 and 2.
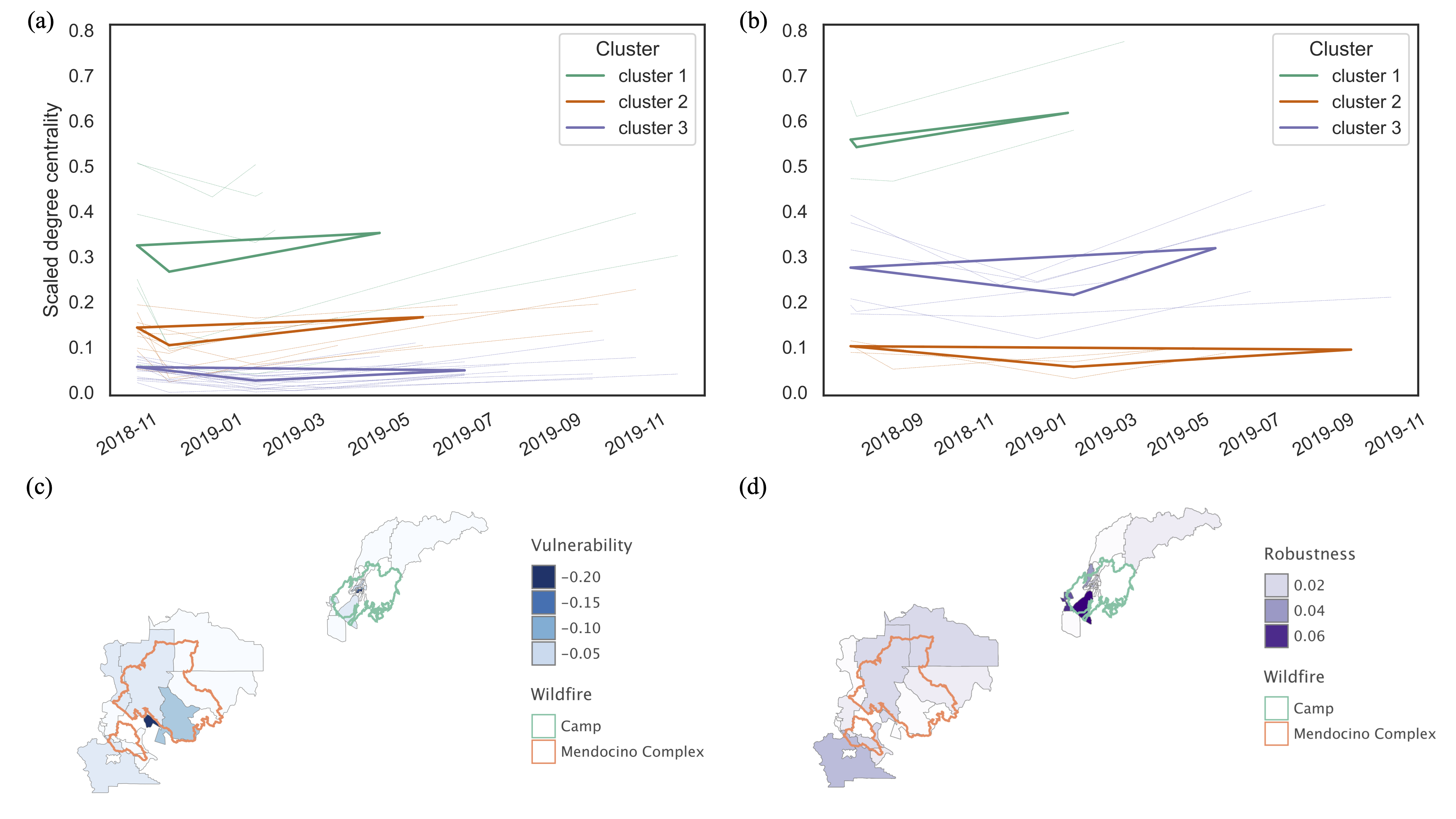
Figure 4. The results of resilience triangles of clustered CBGs and resilience features. (a) The determined resilience triangles of clustered CBGs for Camp wildfire; (b) The determined resilience triangles of clustered CBGs for Mendocino Complex wildfire; (c) Vulnerability of CBGs within the two wildfire areas; (d) Robustness of CBGs within the two wildfires.
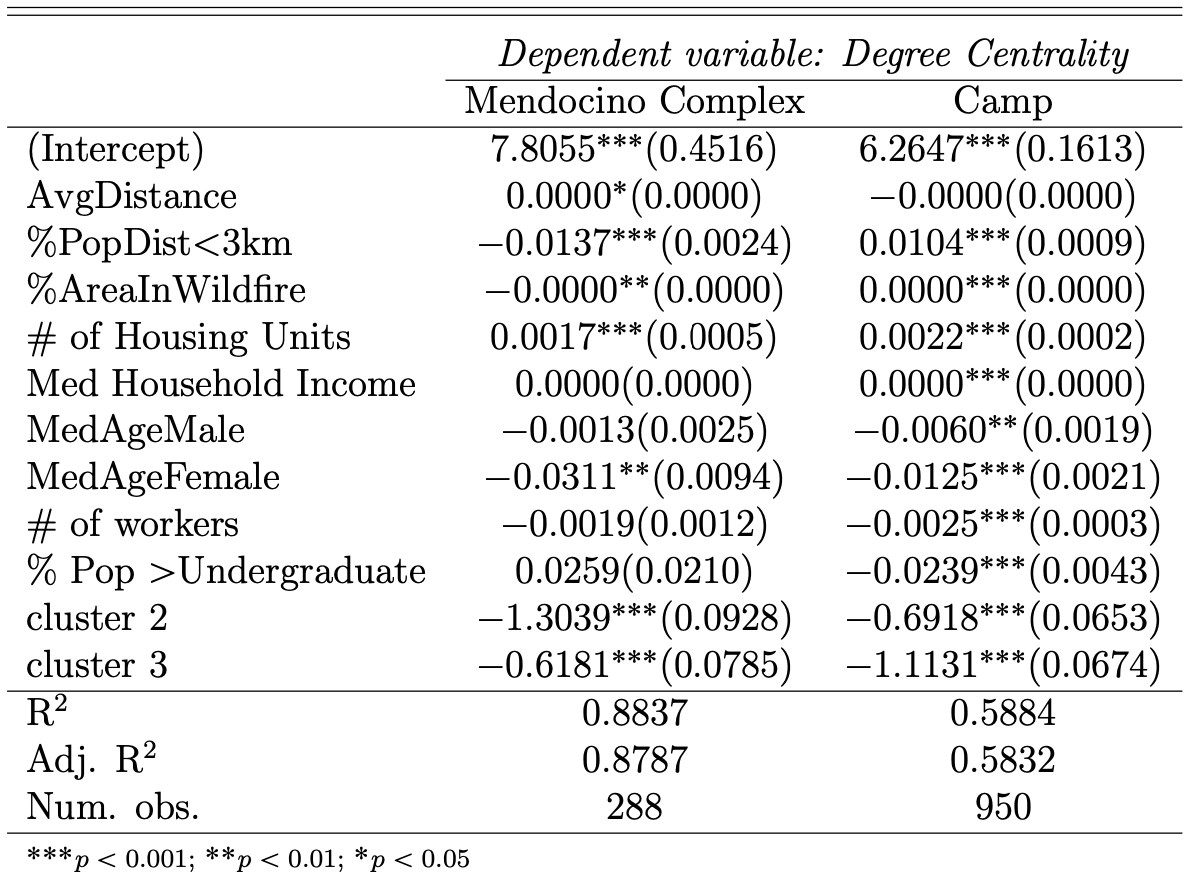
To explain the potential underlying factors related to these clusters, we conduct regression analysis for each wildfire. Table 1 gives a statistical summary of the outcomes of the regression models for the two wildfires. The result shows that the model identifies around 88% of variance of the degree centrality (Adjusted R2 = 0.8787) that is explained by the input variables. Further, most factors, except the number of full-time workers, percentage of people with degree higher than undergraduate, are highly correlated to the degree centrality. For the Camp wildfire, the model shows a relatively weaker ability to identify the variance of the degree centrality explained by the input variables (Adjusted R2 = 0.5832). One possible reason could be that there are much more observations (N = 950) than that in the MC wildfire (N = 288), which can therefore result in more noise in the model.